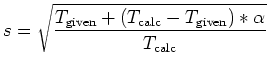23/May/2013
The main features of the development are as follows:
-
(1) NEGF method for the non-collinear DFT (supported by Y. Xiao and T. Ozaki)
-
OpenMX Ver. 3.7 supports the NEGF method coupled with the non-collinear (NC) DFT method,
which can be regarded as a full implementation of NEGF within NC-DFT.
The spin-orbit coupling, the DFT+U method, and the constraint schemes to control
direction of spin and orbital magnetic moments supported for NC-DFT are all compatible
with the implementation of the NEGF method. Thus, it is expected that a wide variety
of problems can be treated, such as transport through magnetic domains with spiral
magnetic structure. The usage of the functionality is basically the same as that for
the collinear DFT case. Related information can be found in the
manual.
-
(2) Improvement of efficiency (supported by T.V.T. Duy, A.M. Ito, and T. Ozaki)
-
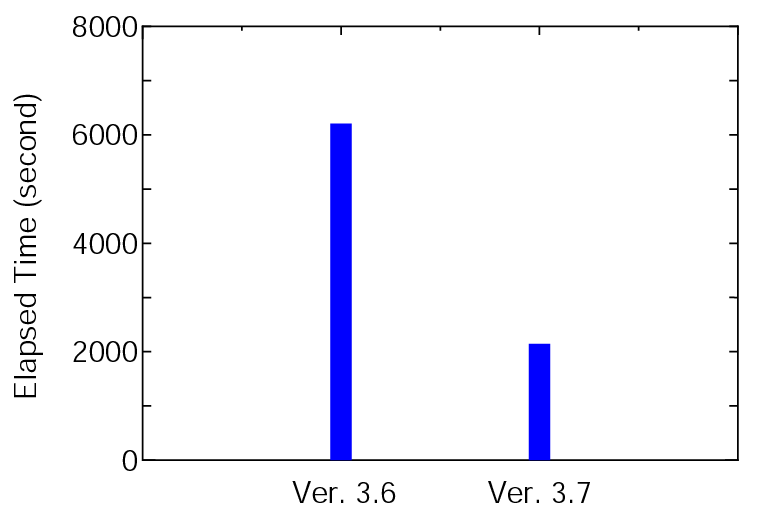
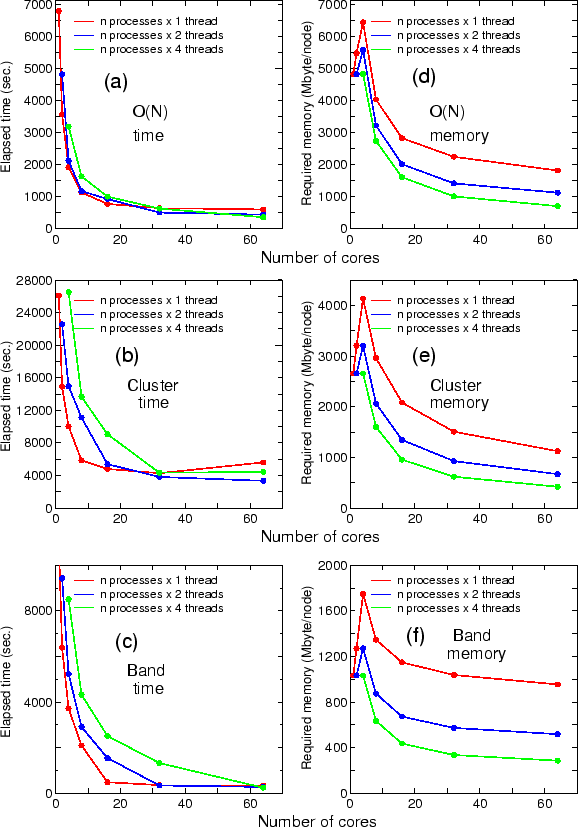
OpenMX Ver. 3.7 outperforms Ver. 3.6 with respect to the computational efficiency.
Most of the program routines being time-consuming have been carefully optimized using several
techniques such as use of BLAS and SSE, unrolling, blocking, and inline expansion.
The elapsed time of runtestL, which is a series of benchmark sets, is shown below:
where 128 MPI processes and 2 OpenMP threads on CRAY-XC30 were used for both the versions. It is found that Ver. 3.7 is about three times faster than Ver. 3.6 for the benchmark sets. The elapsed time for each input file can be confirmed from 'runtestL.result_xc30_v3.6' and 'runtestL.result_xc30' stored in 'work/large_example'.
-
(3) ELPA based parallel eigensolver (supported by T.V.T. Duy and T. Ozaki)
-
OpenMX Ver. 3.7 employs
ELPA1
to solve the eigenvalue problem in the cluster and band calculations,
which is a highly parallelized eigevalue solver. The eigenvalue solver enables us to
perform geometry optimization for systems consisting of 1000 atoms if several hundreds
processor cores are available. To demonstrate the capability, one can perform 'runtestL2'
as follows:
% mpirun -np 128 openmx -runtestL2 -nt 4
Then, OpenMX will run with 7 test files, and compare calculated results with the reference
results which are stored in 'work/large2_example'.
The following is a result of 'runtestL2' performed using 128 MPI processes and 4 OpenMP threads on CRAY-XC30.
| 1 | large2_example/C1000.dat | Elapsed time(s)= 1731.83 | diff Utot= 0.000000002838 | diff Force= 0.000000007504 |
| 2 | large2_example/Fe1000.dat | Elapsed time(s)=21731.24 | diff Utot= 0.000000010856 | diff Force= 0.000000000580 |
| 3 | large2_example/GRA1024.dat | Elapsed time(s)= 2245.67 | diff Utot= 0.000000002291 | diff Force= 0.000000015333 |
| 4 | large2_example/Ih-Ice1200.dat | Elapsed time(s)= 952.84 | diff Utot= 0.000000000031 | diff Force= 0.000000000213 |
| 5 | large2_example/Pt500.dat | Elapsed time(s)= 6831.16 | diff Utot= 0.000000002285 | diff Force= 0.000000004010 |
| 6 | large2_example/R-TiO2-1050.dat | Elapsed time(s)= 2259.97 | diff Utot= 0.000000000106 | diff Force= 0.000000001249 |
| 7 | large2_example/Si1000.dat | Elapsed time(s)= 1655.25 | diff Utot= 0.000000001615 | diff Force= 0.000000005764 |
The quality of all the calculations is at a level of production run where double valence plus a single polarization functions are allocated to each atom as basis functions. Except for 'Pt500.dat', all the systems include more than 1000 atoms, where the last number of the file name implies the number of atoms for each system, and the elapsed time implies that geometry optimization for systems consisting of 1000 atoms is possible if several hundred processor cores are available. It is noted that the parallel eigenvalue solver introduced in OpenMX Ver. 3.7 is not exactly the same as ELPA1 distributed in here. Since we found that the original ELPA1 tends to encounter a numerical instability on some platforms, we modified ELPA1 to make it stabilized. The original parallel eigenvalue solver used in OpenMX Ver. 3.6 is also available by the following keyword:
scf.eigen.lib elpa1 # elpa1|lapack, default=elpa1
One can choose either 'elpa1' or 'lapack' depending on computational environment.
The default is 'elpa1'.
Due to the introduction of the ELPA based eigenvalue solver, users are requested to specify a FORTRAN compiler.
More information can be found in here and here.
-
(4) Massive parallelization of the O(N) Krylov subspace method (supported by T.V.T. Duy and T. Ozaki)
-
The O(N) Krylov subspace method is massively parallelized to realize large-scale calculations of systems
including a hundred thousand atoms. A new parallel algorithm and data structure have been developed
so that the parallel execution can be possible on massively parallel computers consisting of more than
a hundred thousand CPU cores and the data usage can be inversely proportional to the number of MPI processes.
The details of the implementation can be found in
arXiv:1209.4506
and
arXiv:1302.6189v1.
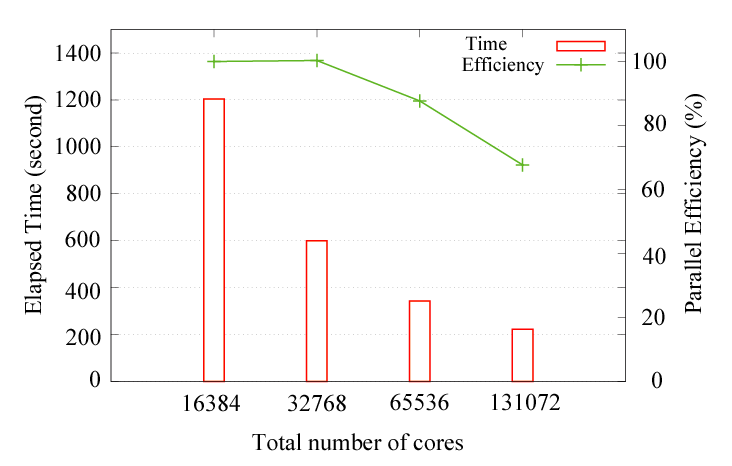
As a benchmark calculation, the parallel efficiency for the hybrid parallelization on the K-computer
is shown below:
where the diamond structure consisting of 131072 carbon atoms was considered as a benchmark system, and eight OpenMP threads were used for all the cases. The parallel efficiency is about 68 % using 131072 cores by taking the case with 16384 cores as a reference. No additional keyword is introduced for the development. The new development has been already applied to two large-scale systems, resulting in two papers: J. Chem. Phys. 136, 134101 (2012) and Modelling Simul. Mater. Sci. Eng. 21, 045012 (2013).
Related information can be found in the manual.
-
(5) Parallelization for k-point (supported by T. Ozaki)
-
Up to and including Ver. 3.6, the number of MPI processes that users can utilize for the parallel calculations
is limited up to the number of atoms in the system. OpenMX Ver. 3.7 does not have the limitation. Even if
the number of MPI processes exceeds the number of atoms, the MPI parallelization is efficiently performed.
The functionality may be useful especially for a calculation where the number of k-points is much larger
than the number of atoms in the system. No additional keyword is introduced for the development.
-
(6) Parallelization for NEB (supported by Y. Kubota and F. Ishii)
-
Although the default parallelization scheme for the NEB calculation works well in most cases, a memory
shortage can be a serious problem when a small number of the MPI processes is used for large-scale systems.
In the default MPI parallelization, the images are preferentially parallelized at first. When the number
of MPI processes exceeds the number of images, the calculation of each image starts to be parallelized,
where the memory usage starts to be parallelized as well. In this case, users may encounter a segmentation
fault due to the memory shortage if many CPU cores are not available. To avoid such a situation, the following
keyword is available.
MD.NEB.Parallel.Number 3
In this example, the calculations of every three images are parallelized at once where the MPI processes
are classified to three groups and utilized for the parallelization of each image among the three images.
In order to complete the calculations of all the images, the grouped calculations are repeated
by floor[(the number of images)/(MD.NEB.Parallel.Number)] times. The scheme may be useful for the NEB
calculation of a large-scale system. If the keyword is not specified in your input file, the default
parallelization scheme is employed.
Related information can be found in the
manual.
-
(7) Compatibility with the database Ver. 2013 of VPS and PAO (supported by T. Ozaki)
-
The database Ver. 2013 of VPS and PAO was tested with OpenMX Ver. 3.7.
One can reproduce the same result shown in the database using input files
provided on the same web site.
Some more information can be found in the
manual.
-
(8) Other changes are listed below:
-
Specification of FORTRAN compiler:
manual and
manual
-
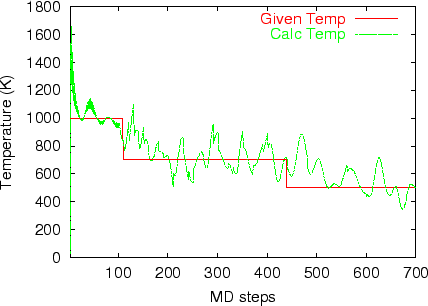
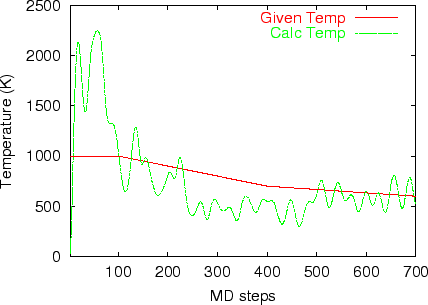
Multi-heat bath molecular dynamics:
manual.
-
Fully three dimensional parallelization:
manual.
-
Delta factor:
manual.
-
Analysis of memory usage:
manual.
-
Output of large-sized files in binary mode:
manual.
-
(9) Bugs fixed
-
Minor bugs in OpenMX Ver. 3.6 were fixed.
-
(10) Manual revised
-
The manual of OpenMX was revised.
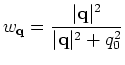
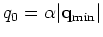
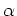 .
Then, the following keyword is available.
.
Then, the following keyword is available.