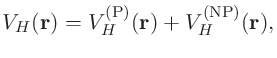 |
(15) |
ここではTiC固体を例として、固体系における内殻準位の絶対束縛エネルギーの計算方法を説明します。
始状態の計算は以下のように実行します。
% mpirun -np 112 ./openmx TiC216.dat | tee TiC216.std
ここで、特別なキーワードは指定しませんが、
「scf.SpinPolarization=on」としてスピン分極計算が実行されます。ここでのスピン分極計算は
終状態の計算と整合性を取るために実施されています。ただし計算結果は非磁性となります。
ここで用いた入力ファイル「TiC216.dat」はディレクトリ「work」に収容されています。
終状態の計算は以下のように実行します。
% mpirun -np 112 ./openmx TiC216-CH3.dat | tee TiC216-CH3.std
ここで用いた入力ファイル「TiC216-CH3.dat」はディレクトリ「work」に収容されています。
この入力ファイル中で原子種は以下のように定義されています。
<Definition.of.Atomic.Species
Ti Ti7.0-s3p2d2 Ti_PBE13
C C6.0_1s-s3p2d1 C_PBE17_1s
C1 C6.0_1s_CH-s3p2d1 C_PBE17_1s
Definition.of.Atomic.Species>
そして、以下のように原子種「C1」が原子5に割り当てられます。
Atoms.Number 216
Atoms.SpeciesAndCoordinates.Unit Ang # Ang|AU
<Atoms.SpeciesAndCoordinates
1 Ti 0.000000000000 0.000000000000 0.000000000000 6.0 6.0
2 Ti 2.163500000000 2.163500000000 0.000000000000 6.0 6.0
3 Ti 0.000000000000 2.163500000000 2.163500000000 6.0 6.0
4 Ti 2.163500000000 0.000000000000 2.163500000000 6.0 6.0
5 C1 2.163500000000 0.000000000000 0.000000000000 3.0 3.0
6 C 0.000000000000 2.163500000000 0.000000000000 3.0 3.0
7 C 0.000000000000 0.000000000000 2.163500000000 3.0 3.0
8 C 2.163500000000 2.163500000000 2.163500000000 3.0 3.0
....
..
Atoms.SpeciesAndCoordinates>
以下のキーワードを指定することで、原子5の
scf.restart on
scf.restart.filename TiC216
scf.coulomb.cutoff on
scf.core.hole on
scf.system.charge 0.0 # default=0.0
<core.hole.state
5 s 1
core.hole.state>
終状態の計算においてHartreeポテンシャル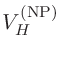 です。
です。
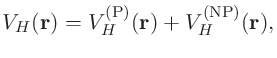 |
(15) |
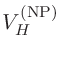 は差電荷密度
は差電荷密度
始状態と終状態の計算を終えると、出力ファイルから全エネルギーが得られます。
Initial state: -10499.900104007471 (Hartree)
Final state: -10489.553360141708 (Hartree)
そして、式 (14)を用いて、束縛エネルギーが以下のとおり計算できます。
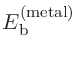 |
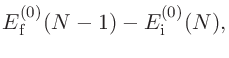 |
||
![\includegraphics[width=16.0cm]{XPS-Fig2.eps}](XPS-Fig2.png)
|
ギャップのある系の他の例として、固体シリコンの計算を説明します。 始状態と終状態の計算を以下のように実行します。
% mpirun -np 256 ./openmx Si-4-SOI.dat | tee Si-4-SOI.std
% mpirun -np 256 ./openmx Si-4-CH-SOI1.dat | tee Si-4-CH-SOI1.std
% mpirun -np 256 ./openmx Si-4-CH-SOI6.dat | tee Si-4-CH-SOI6.std
scf.SpinPolarization nc # On|Off|NC
scf.SpinOrbit.Coupling on # On|Off, default=off
始状態と終状態の計算を終えると、出力ファイルから全エネルギーが得られます。
Initial state: -34820.483255130872 (Hartree)
Final state for SOI1: -34816.628201335407 (Hartree)
Final state for SOI6: -34816.601864921540 (Hartree)
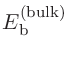 |
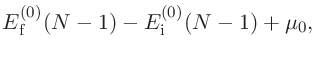 |
||
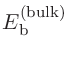 |
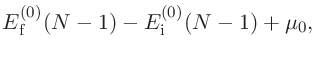 |
||
![]() と
と ![]() に対する99.41 と 100.13 eVの束縛エネルギー値は
実験値の99.2と99.8eV [92]と比較して良い一致が見られます。
ここで、
に対する99.41 と 100.13 eVの束縛エネルギー値は
実験値の99.2と99.8eV [92]と比較して良い一致が見られます。
ここで、![]() と
と ![]() の縮重度は表12に記載されるようにそれぞれ4と2です。
ギャップのある系では単位胞サイズに対する絶対束縛エネルギーの収束性は遅いです。
図78(a)と(b)ではそれぞれギャップのある系と金属での相対束縛エネルギーを
内殻ホール間距離の関数として示しています。
ギャップのある系では収束が遅く、収束値を得るために大きなスーパーセルが必要であることを意味しています。
一方、金属では小さな内殻ホール間距離において束縛エネルギーが速やかに収束していることが分かります。
図 78(c)に
の縮重度は表12に記載されるようにそれぞれ4と2です。
ギャップのある系では単位胞サイズに対する絶対束縛エネルギーの収束性は遅いです。
図78(a)と(b)ではそれぞれギャップのある系と金属での相対束縛エネルギーを
内殻ホール間距離の関数として示しています。
ギャップのある系では収束が遅く、収束値を得るために大きなスーパーセルが必要であることを意味しています。
一方、金属では小さな内殻ホール間距離において束縛エネルギーが速やかに収束していることが分かります。
図 78(c)に![]() 状態への内殻ホールの生成により誘起された固体シリコンでの差電荷密度を示します。
内殻ホールにより生成されたポテンシャルを遮蔽するため、内殻ホールから約
状態への内殻ホールの生成により誘起された固体シリコンでの差電荷密度を示します。
内殻ホールにより生成されたポテンシャルを遮蔽するため、内殻ホールから約![]() Åの周辺まで電荷の再配置が発生します。
ギャップのある系で見られた遅い収束は電荷の遠距離に渡る電荷の再配置が原因となっています。
他方、金属では電荷の再配置は比較的、狭い範囲に限定され、
このため図 78(b)に示したように早い収束を達成されています。
Åの周辺まで電荷の再配置が発生します。
ギャップのある系で見られた遅い収束は電荷の遠距離に渡る電荷の再配置が原因となっています。
他方、金属では電荷の再配置は比較的、狭い範囲に限定され、
このため図 78(b)に示したように早い収束を達成されています。
計算の他の例題と計算に用いた入力ファイルはウェブサイト
https://t-ozaki.issp.u-tokyo.ac.jp/vps_pao_core2019/
で公開されていますので、参考にして下さい。
また、本手法の応用例(シリコン、ボロフェン、グラフェン上に分散されたプラチナ単原子)が
文献[93,94,95] で議論されています。