Absolute binding energies of core levels in solids from first-principles
The original has been published in Phys. Rev. Let. 118, 026401 (2017).

Abstract

A general method is presented to calculate absolute binding energies of core levels in metals and insulators, based on a penalty functional and an exact Coulomb cutoff method in a framework of the density functional theory. The spurious interaction of core holes between supercells is avoided by the exact Coulomb cutoff method, while the variational penalty functional enables us to treat multiple splittings due to chemical shift, spin-orbit coupling, and exchange interaction on equal footing, both of which are not accessible by previous methods. It is demonstrated that the absolute binding energies of core levels for both metals and insulators are calculated by the proposed method in a mean absolute (relative) error of 0.4 eV (0.16 %) for eight cases compared to experimental values measured with X-ray photoemission spectroscopy within a generalized gradient approximation to the exchange-correlation functional.

Since the pioneering works by Siegbahn et al. [1, 2], the X-ray photoelectron spectroscopy (XPS) has become one of the most important and widely used techniques in studying chemical composition and electronic states in the vicinity of surfaces of materials [3]. Modern advances combined with synchrotron radiation further extend its usefulness to enable a wide variety of analyses such as core level vibrational fine structure [4], magnetic circular dichroism (MCD) [5], spin-resolved XPS [6], and photoelectron holography [7]. The basic physics behind the still advancing XPS measurements is dated back to the first interpretation for the photoelectric effect by Einstein [8]. An incident X-ray photon excites a core electron in a bulk, and the excited electron with a kinetic energy is emitted from the surface to vacuum. The binding energy of the core level in the bulk can be obtained by measuring the kinetic energy [1, 2]. Theoretically, the calculation of the binding energy involving evaluation of the total energies for the initial and final states is still a challenging issue especially for insulators, since after the emission of the photoelectron the system is not periodic anymore and ionized due to the creation of the core hole. The violation of the periodicity hampers use of conventional electronic structure methods under a periodic boundary condition, and the Coulomb potential of the ionized bulk cannot be treated under an assumption of the periodicity due to the Coulombic divergence. One way to avoid the Coulombic divergence is to neutralize the final state with a core hole by adding an excess electron into conduction bands [9, 10, 11, 12, 13] or to approximate the bulk by a cluster model [14]. However, the charge compensation may not occur in insulators because of the short escape time of photoelectron ($\sim {10}^{-16}$ sec.) [15], while the treatment might be justified for metals. Even if we employ the charge compensation scheme, the screened core hole pseudopotential which has been widely used in pseudopotential methods allows us to calculate only the chemical shift of binding energies, but not the absolute values [9]. In spite of the long history of XPS and its importance in materials science, a general method has not been developed so far to calculate the absolute binding energies for both insulators and metals, including multiple splittings due to chemical shift, spin-orbit coupling, and exchange interaction, on equal footing [16]. In this Letter we propose a general method to calculate absolute binding energies of core levels in metals and insulators, allowing treatment of all the issues mentioned above and the direct comparison to experimental results, in a single framework within the density functional theory (DFT) [19, 20].

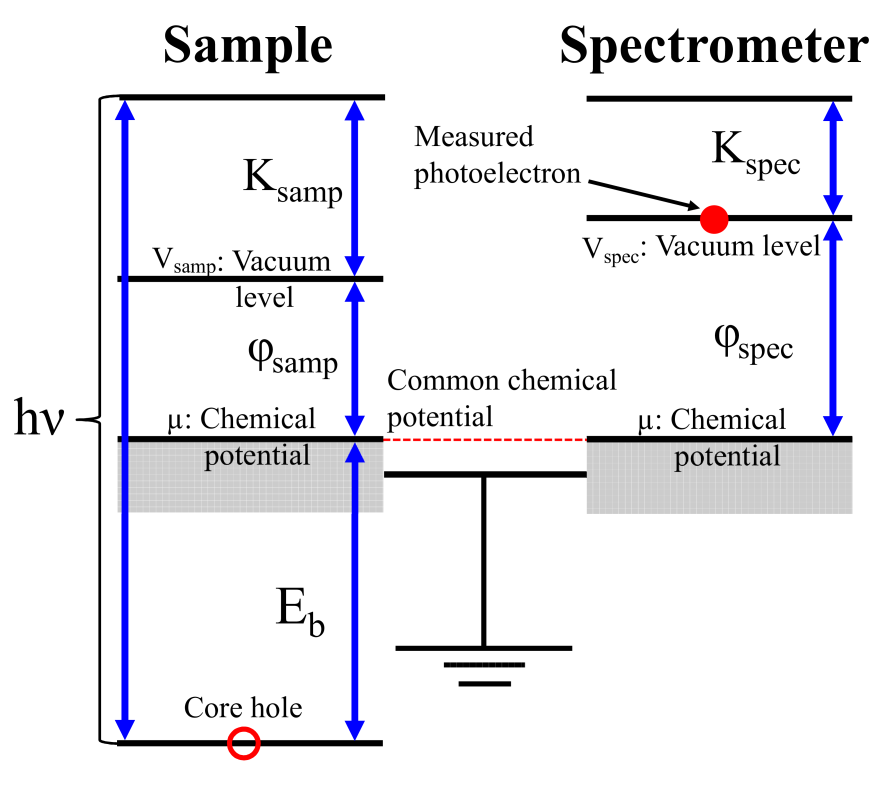
Figure 1: Schematic energy diagram for a sample and a spectrometer in the XPS measurement.

Let us start to define the absolute binding energy $E_{\mathrm{b}}$ of core electrons in bulks measured by a XPS experiment, based on the energy conservation. The energy of the initial state is given by the sum of the total energy $E_{\mathrm{i}}(N)$ of the ground state of $N$ electrons and an energy $h\nu$ of a monochromatic X-ray photon. On the other hand, that of the final state is contributed by the total energy $E_{\mathrm{f}}(N-1)$ of the excited state of $N-1$ electrons with a core hole, and the kinetic energy $K_{\mathrm{spec}}$ of photoelectron placed at the vacuum level $V_{\mathrm{spec}}$ as shown in Fig. 1. Therefore, the energy conservation in the XPS measurement is expressed by

$E_{\mathrm{i}}(N)+h\nu =E_{\mathrm{f}}(N-1)+V_{\mathrm{spec}}+K_{\mathrm{spec}}.$ (1)

Noting that the chemical potential of sample is aligned with that of the spectrometer $\mu$ by Ohmic contact, and that the vacuum level of the spectrometer $V_{\mathrm{spec}}$ is given by $V_{\mathrm{spec}}=\mu +{\phi }_{\mathrm{spec}}$ using the work function of the spectrometer ${\phi }_{\mathrm{spec}}$, Eq. (1) reads to

$h\nu -K_{\mathrm{spec}}-{\phi }_{\mathrm{spec}}=E_{\mathrm{f}}(N-1)-E_{\mathrm{i}}(N)+\mu .$ (2)

The left hand side of Eq. (2) is the binding energy $E_{\mathrm{b}}^{(\mathrm{bulk})}$ measured by the XPS experiment [21]. The right hand side of Eq. (2) provides a useful expression to calculate the absolute binding energy $E_{\mathrm{b}}^{(\mathrm{bulk})}$ for bulks regardless of the band gap of materials. Instead of using the experimental chemical potential $\mu$, it is possible to rewrite the total energies with the intrinsic chemical potential ${\mu }_0$, where intrinsic means a state which is free from the control of chemical potential, by noting that what the shift of chemical potential $\mu ={\mu }_0+\mathrm{\Delta }\mu$ does is only the constant shift of potential $\mathrm{\Delta }\mu$. Then, we rewrite them as $E_{\mathrm{i}}(N)=E_{\mathrm{i}}^{(0)}(N)+N\mathrm{\Delta }\mu$ and $E_{\mathrm{f}}(N-1)=E_{\mathrm{f}}^{(0)}(N-1)+(N-1)\mathrm{\Delta }\mu$ using the intrinsic total energies $E_{\mathrm{i}}^{(0)}(N)$ and $E_{\mathrm{f}}^{(0)}(N-1)$ by assuming the common chemical potential $\mu$ for both the initial and final states due to a very large $N$. Inserting these equations into Eq. (2) yields

$E_{\mathrm{b}}^{(\mathrm{bulk})}=E_{\mathrm{f}}^{(0)}(N-1)-E_{\mathrm{i}}^{(0)}(N)+{\mu }_0.$ (3)

Equation (3) is an important consequence, since only quantities which can be calculated from first-principles are involved. Thereby, we use Eq. (3) to calculate the absolute binding energy $E_{\mathrm{b}}^{(\mathrm{bulk})}$. Note that the chemical potential ${\mu }_0$ is calculated by assuming the Fermi distribution at a finite electronic temperature. It should be emphasized that Eq. (3) is valid even for semi-conductors and insulators. In an arbitrary gapped system, the common chemical potential $\mu$ is pinned at either the top of valence band or the bottom of conduction band, or located in between them. For all the possible cases, the exactly same discussion above is valid. Thus, we conclude that Eq. (3) is a general formula to calculate the absolute binding energy $E_{\mathrm{b}}^{(\mathrm{bulk})}$ of solids. Especially for metals, Eq. (3) can be further reorganized by noting a rigorous relation derived with the Janak theorem [23]: $E_{\mathrm{f}}^{(0)}(N-1)-E_{\mathrm{f}}^{(0)}(N)=\int 𝑑n\partial E_{\mathrm{f}}^{(0)}/\partial n=-{\mu }_0$, where $n$ is an occupation number of an one-particle eigenstate on the Fermi surface, $dn=-ds/S$ defined with the area of the Fermi surface $S$ and an infinitesimal area $ds$, and the surface integral is performed over the Fermi surface. By inserting the above equation into Eq. (3), we obtain the following formula:

$E_{\mathrm{b}}^{(\mathrm{metal})}=E_{\mathrm{f}}^{(0)}(N)-E_{\mathrm{i}}^{(0)}(N),$ (4)

which allows us to employ the total energy of the neutralized final state $E_{\mathrm{f}}^{(0)}(N)$ instead of that of the ionized state. For metals, Eqs. (3) and (4) should result in an equivalent binding energy in principle, however, the convergence is different from each other as a function of the system size as shown later on.

Since $E_{\mathrm{i}}^{(0)}(N)$ and ${\mu }_0$ in Eq. (3) can be calculated by a conventional approach with the periodic boundary condition, we now turn to discuss a method of calculating $E_{\mathrm{f}}^{(0)}(N-1)$ in Eq. (3) based on the total energy calculation including many body effects. Core electrons for which a core hole is created are explicitly included in the calculations to treat multiple splittings due to chemical shift, spin-orbit coupling, and exchange interaction between core and spin-polarized valence electrons, and to take account of many body screening effects. The creation of the core hole can be realized by expressing the total energy of the final state by the sum of a conventional total energy $E_{\mathrm{DFT}}$ within DFT and a penalty functional $E_{\mathrm{pen}}$ as

$E_{\mathrm{f}}^{(0)}(N-1)=E_{\mathrm{DFT}}+E_{\mathrm{pen}}$ (5)

with the definition of $E_{\mathrm{pen}}$:

$E_{\mathrm{pen}}={\displaystyle \frac{1}{V_{\mathrm{B}}}}{\displaystyle {\int }_{\mathrm{B}}}𝑑k^3{\displaystyle \sum _{\mu }}{f}_{\mu }^{(𝐤)}⟨{\psi }_{\mu }^{(𝐤)}|\widehat{P}|{\psi }_{\mu }^{(𝐤)}⟩,$ (6)

where ${\int }_{\mathrm{B}}𝑑k^3$ is the integration over the first Brillouin zone whose volume is $V_{\mathrm{B}}$, $f_{\mu }^{(𝐤)}$ the Fermi function, and ${\psi }_{\mu }^{(𝐤)}$ the Kohn-Sham wave function of two-component spinor. In Eq. (6) the projector $\widehat{P}$ is defined with an angular eigenfunction $\mathrm{\Phi }$ of the Dirac equation under a spherical potential and a radial eigenfunction $R$ obtained by an atomic DFT calculation for the Dirac equation as

$\widehat{P}\equiv |R{\mathrm{\Phi }}_J^M⟩\mathrm{\Delta }⟨R{\mathrm{\Phi }}_J^M|$ (7)

with for $J=l+\frac{1}{2}$ and $M=m+\frac{1}{2}$

$|{\mathrm{\Phi }}_J^M⟩$ $=$ ${\left({\displaystyle \frac{l+m+1}{2l+1}}\right)}^{\frac{1}{2}}|Y_l^m\alpha ⟩+{\left({\displaystyle \frac{l-m}{2l+1}}\right)}^{\frac{1}{2}}|Y_l^{m+1}\beta ⟩,$ (8)

and for $J=l-\frac{1}{2}$ and $M=m-\frac{1}{2}$

$|{\mathrm{\Phi }}_J^M⟩$ $=$ ${\left({\displaystyle \frac{l-m+1}{2l+1}}\right)}^{\frac{1}{2}}|Y_l^{m-1}\alpha ⟩-{\left({\displaystyle \frac{l+m}{2l+1}}\right)}^{\frac{1}{2}}|Y_l^m\beta ⟩,$ (9)

where $Y$ is a spherical harmonic function, and $\alpha$ and $\beta$ spin basis functions. The variational treatment of Eq. (5) with respect to $\psi$ leads to the following Kohn-Sham equation:

$\left(\widehat{T}+v_{\mathrm{eff}}+\widehat{P}\right)|{\psi }_{\mu }^{(𝐤)}⟩={\epsilon }_{\mu }^{(𝐤)}|{\psi }_{\mu }^{(𝐤)}⟩,$ (10)

where $\widehat{T}$ is the kinetic operator, and $v_{\mathrm{eff}}$ the conventional KS effective potential originated from $E_{\mathrm{DFT}}$. If a large number, 100 Ryd. was used in this study, is assigned for $\mathrm{\Delta }$ in Eq. (7), the targeted core state ${\mathrm{\Phi }}_J^M$ specified by the quantum numbers $J$ and $M$ is penalized through the projector $\widehat{P}$ in Eq. (10), and becomes unoccupied, resulting in the creation of a core hole for the targeted state. Since the creation of the core hole is self-consistently performed, the screening effects by both core and valence electrons, spin-orbit coupling, and exchange interaction are naturally taken into account in a single framework. It is also straightforward to reduce the projector $\widehat{P}$ to the non-relativistic treatment.

After the creation of the core hole, the final state has one less electron, leading to charging of the system. In the periodic boundary condition, a charged system cannot be treated in general because of the Coulombic divergence. The neutralization of the final state may occur in a metal, and theoretically such a neutralization can be justified as shown by Eq. (4). However, it is unlikely that such a charge compensation takes place in an insulator during the escape time of photoelectron ($\sim {10}^{-16}$ sec.) [15]. To overcome the difficulty, we propose a general method of treating the charged state based on an exact Coulomb cutoff method [24]. It is considered that the created core hole is isolated in the sample, resulting in violation of the periodicity of the system. The isolation of the core hole can be treated by dividing the charge density ${\rho }_{\mathrm{f}}(𝐫)$ for the final state into a periodic part ${\rho }_{\mathrm{i}}(𝐫)$ and a non-periodic part $\mathrm{\Delta }\rho (𝐫)(\equiv {\rho }_{\mathrm{f}}(𝐫)-{\rho }_{\mathrm{i}}(𝐫))$ which, when integrated over the unit cell, is exactly -1, where ${\rho }_{\mathrm{i}}(𝐫)$ is the charge density for the initial state without the core hole. Then, as shown in Fig. 2(a) the Hartree potential $V_{\mathrm{H}}(𝐫)$ in the final state is given by

$V_{\mathrm{H}}(𝐫)=V_{\mathrm{H}}^{(\mathrm{P})}(𝐫)+V_{\mathrm{H}}^{(\mathrm{NP})}(𝐫),$ (11)

where $V_{\mathrm{H}}^{(\mathrm{P})}(𝐫)$ is the periodic Hartree potential calculated using the periodic part ${\rho }_{\mathrm{i}}(𝐫)$ via a conventional method using a fast Fourier transform (FFT) for the Poisson equation. On the other hand, the non-periodic Hartree potential $V_{\mathrm{H}}^{(\mathrm{NP})}(𝐫)$ is calculated using $\mathrm{\Delta }\rho (𝐫)$ and an exact Coulomb cutoff method by

$V_{\mathrm{H}}^{(\mathrm{NP})}(𝐫)={\displaystyle \sum _{𝐆}}\widetilde{\mathrm{\Delta }\rho }(𝐆)\tilde{v}(𝐆){\mathrm{e}}^{i𝐆\cdot 𝐫},$ (12)

where $\widetilde{\mathrm{\Delta }\rho }(𝐆)$ is the discrete Fourier transform of $\mathrm{\Delta }\rho (𝐫)$, and $\tilde{v}(𝐆)$ is given by $\frac{4\pi }{G^2}(1-\cos (G{R}_{\mathrm{c}}))$, which is the Fourier transform of a cutoff Coulomb potential with the cutoff radius of $R_{\mathrm{c}}$ [24]. If $\mathrm{\Delta }\rho (𝐫)$ is localized within a sphere of a radius $R$ as shown in Fig. 2(b), the extent of the Coulomb interaction is $2R$ at most in the sphere, which leads to $R_{\mathrm{c}}=2R$. In addition, a condition should be satisfied to avoid the spurious interaction between the core holes. In practice, we set $R_{\mathrm{c}}=\frac{1}{2}L$, and investigate the convergence of the binding energy as a function of $L$. With the treatment the core hole is electrostatically isolated from the other periodic images of the core hole even under the periodic boundary condition.

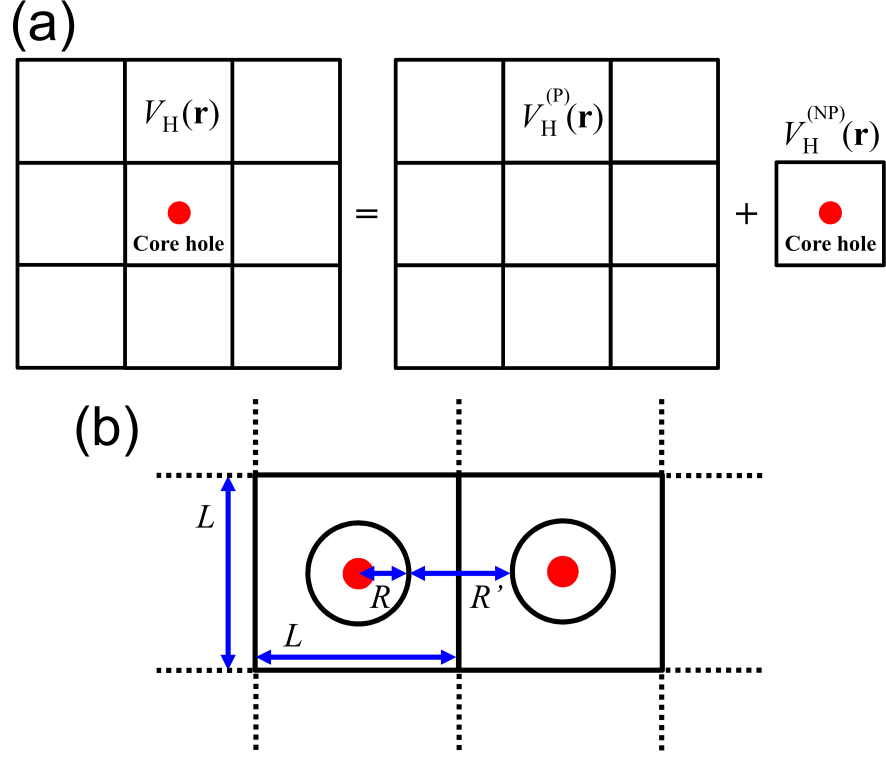
Figure 2: (a) Treatment of the Hartree potential in a system with a core hole under the periodic boundary condition. (b) Configuration to calculate the non-periodic part of the Hartree potential $V_{\mathrm{H}}^{(\mathrm{NP})}$ by the exact Coulomb cutoff method for $\mathrm{\Delta }\rho$.

We implemented the method in a DFT software package OpenMX [25], which is based on norm-conserving relativistic pseudopotentials [26, 27] and pseudo-atomic basis functions [28]. A generalized gradient approximation (GGA) [29] to the exchange-correlation functional and an electronic temperature of 300 K were used. The details of implementation are given in the supplemental material [35]. All the molecular and crystal structures used in the study were taken from experimental ones.

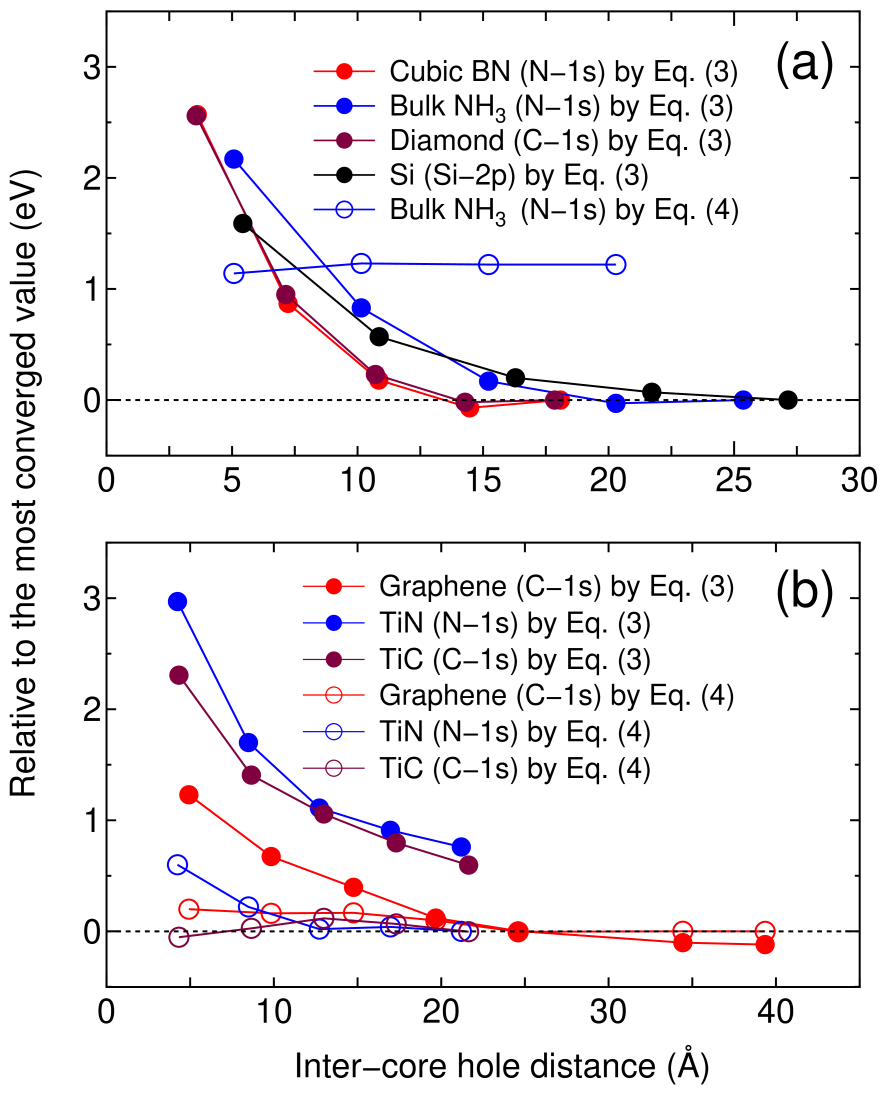
Figure 3: Calculated binding energies, relative to the most converged value, of (a) gapped systems and (b) a semimetal (graphene) and metals as a function of inter-core hole distance. The reference binding energies in (a) and (b) were calculated by Eqs. (3) and (4), respectively, for the largest unit cell for each system.

Figures 3(a) and (b) show relative binding energies of core levels in gapped systems and metals including a semimetal (graphene), respectively, as a function of inter-core hole distance. For the gapped systems the convergent results are obtained at the inter-core hole distance of $\sim$ 15, 20, and 27 Å for cubic boron nitride (diamond), bulk NH${}_3$, and silicon, respectively. This implies that the difference charge $\mathrm{\Delta }\rho (𝐫)$ induced by the creation of the core hole is localized within a sphere with a radius of $R=L/4$, e.g., $\sim$ 7 Å for silicon. In fact, the localization of $\mathrm{\Delta }\rho (𝐫)$ in silicon can be confirmed by the distribution in real space and the radial distribution of a spherically averaged $\mathrm{\Delta }\rho$ as shown in Figs. 4(a) and (b). The deficiency of electron around 0.3 Å corresponding to the core hole in the $2p$-states is compensated by increase of electron density around 1 Å, which is the screening on the same silicon atom for the core hole. As a result of the short range screening, the non-periodic Hartree potential $V_{\mathrm{H}}^{(\mathrm{NP})}(𝐫)$ deviates largely from $-1/r$ as shown in Fig. 4(c).

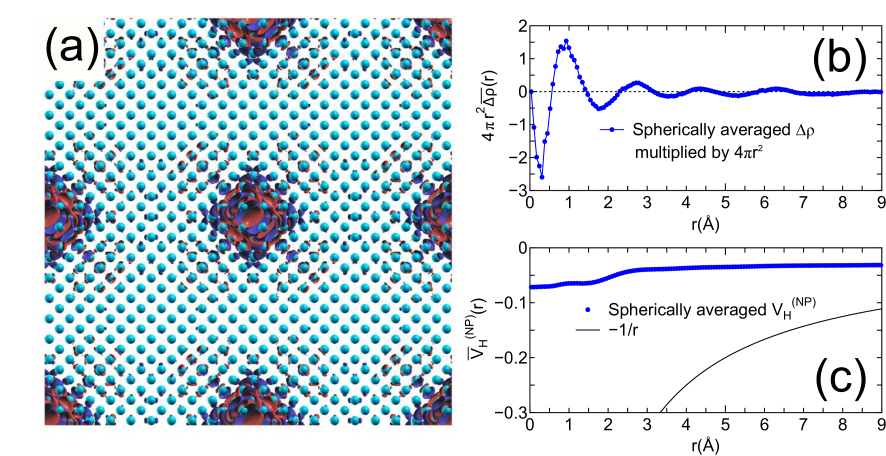
Figure 4: (a) Difference charge density $\mathrm{\Delta }\rho$ in silicon, induced by the creation of a core hole in the $2p$-states, where the unit cell contains 1000 atoms, and the inter-core hole distance is 27.15 Å. (b) Radial distribution of $4\pi r^2\overline{\mathrm{\Delta }\rho }$, where $\overline{\mathrm{\Delta }\rho }$ is a spherically averaged $\mathrm{\Delta }\rho$. (c) Radial distribution of ${\overline{V}}_{\mathrm{H}}^{(\mathrm{NP})}$ being a spherically averaged $V_{\mathrm{H}}^{(\mathrm{NP})}$.

In Fig. 3(a) it is also shown that the binding energy of the bulk NH${}_3$ calculated with Eq. (4) converges at 1.2 eV above, implying that Eq. (4) cannot be applied to gapped systems. On the other hand, for the metallic cases we see that Eq. (4) provides a much faster convergence than Eq. (3), and both Eqs. (3) and (4) seem to give a practically equivalent binding energy, while the results calculated with Eq. (3) for TiN and TiC do not reach to the sufficient convergence due to computational limitation [34]. Therefore, Eq. (4) is considered to be the choice for the practical calculation of a metallic system because of the faster convergence. By compiling the size of the unit cell achieving the convergence into the number of atoms in the unit cell, the use of a supercell including $\sim$ 500 and 64 atoms for gapped and metallic systems in three-dimensions might be a practical guideline for achieving a sufficient convergence by using Eqs. (3) and (4), respectively. The calculated values of binding energies are well compared with the experimental absolute values as shown in Table 1 for both the gapped and metallic systems, and the mean absolute (relative) error is found to be 0.4 eV (0.16 %) for the eight cases. We see that the splitting due to spin-orbit coupling in the silicon $2p$-states is well reproduced. In addition, binding energies of a core level for gaseous molecules are shown in the supplemental material, where the mean absolute (relative) error is found to be 0.5 eV (0.22 %) for the 23 cases.

Table 1: Calculated binding energy of a core level in bulks.

Material	State	Calc. (eV)	Expt. (eV)
Gapped system
c-BN	N-$1s$	398.87	398.1${}^{*}$
bulk NH${}_3$	N-$1s$	398.92	399.0${}^{+}$
Diamond	C-$1s$	286.50	285.6${}^{†}$
Si	Si-$2p_{1/2}$	100.13	99.8${}^{*}$
Si	Si-$2p_{3/2}$	99.40	99.2${}^{*}$
Semimetal or Metal
Graphene	C-$1s$	284.23	284.4${}^{†}$
TiN	N-$1s$	396.43	397.1${}^{\mathrm{\S }}$
TiC	C-$1s$	281.43	281.5${}^{*}$

${}^{*}$ Ref. [30], ${}^{+}$ Ref. [31], ${}^{†}$ Ref. [32] (graphite), ${}^{\mathrm{\S }}$ Ref. [33]

In summary, we proposed a general method to calculate absolute binding energies of core levels in metals and insulators in a framework of DFT. The method is based on a penalty functional and an exact Coulomb cutoff method. The former allows us to calculate multiple splittings due to chemical shift, spin-orbit coupling, and exchange interaction, while the latter enables us to treat a charged system with a core hole under the periodic boundary condition. It was also shown that especially for metals Eq. (4) involving the neutralized final state is equivalent to Eq. (3) involving the ionized final state, and that Eq. (4) is computationally more efficient than Eq. (3). The remarkable agreement with the absolute binding energies measured in XPS demonstrates the validity of the proposed method for a variety of materials. For a better description of a case where an exchange interaction plays a dominant role in the splitting, a good approximation to the exchange-correlation functional should be adopted and our method provides a natural way to examine the resulting total energies, while a possible error by the pseudopotentials and the dependency of chemical potential on surface structures should also be addressed in future work. Considering the importance of the XPS measurement in materials researches, the proposed method is anticipated to play an indispensable role in quantitatively analyzing absolute binding energies of core levels in solids.