摂動論に基づくLiechtensteinの方法 [17]を用いて局在したスピン間の交換結合パラメタ![]() を計算できます。
この計算はポストプロセスのプログラム「jx」を用いて実行します。
OpenMX Ver 3.9において本機能はクラスタやバルク系のコリニアDFT計算のみに有効で、ノンコリニアDFT計算には一般化されていません。
本機能を用いて論文等を出版される場合は文献[18,19]を引用して頂けますと幸いです。
を計算できます。
この計算はポストプロセスのプログラム「jx」を用いて実行します。
OpenMX Ver 3.9において本機能はクラスタやバルク系のコリニアDFT計算のみに有効で、ノンコリニアDFT計算には一般化されていません。
本機能を用いて論文等を出版される場合は文献[18,19]を引用して頂けますと幸いです。
このプログラム「jx」は![]() を計算する以下の三つの方法を提供します。
を計算する以下の三つの方法を提供します。
クラスタ系に対して、本プログラム「jx」は以下の表式に基づき原子サイト![]() と
と![]() の間の交換結合定数
の間の交換結合定数![]() を計算します。
を計算します。
![$[\hat{P}_{i}]_{\nu\mu}$](img238.png) と
と
![$[\hat{P}_{j}]_{\nu'\mu'}$](img239.png) は
サイト
は
サイト
バルク系に対して、本プログラム「jx」は以下の表式に基づきセル ![]() と
と ![]() にそれぞれ
位置する原子サイト
にそれぞれ
位置する原子サイト ![]() と
と ![]() の間の交換結合定数
の間の交換結合定数
![]() を計算します。
を計算します。
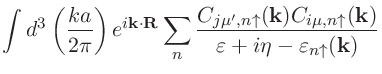 |
(6) | ||
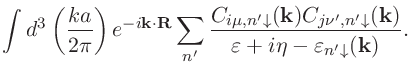 |
(7) |
交換結合![]() の
の![]() に渡る総和を考慮する場合には以下の表式を用いて計算することもできます。
に渡る総和を考慮する場合には以下の表式を用いて計算することもできます。
Flag.PeriodicSumを指定することでどちらかの計算が選択できます。