NVT molecular dynamics by a velocity scaling (NVT_VS)
A velocity scaling scheme [30] is supported to perform
NVT ensemble molecular dynamics simulations by the following keyword:
MD.Type NVT_VS # NOMD|Opt|NVE|NVT_VS|NVT_VS2|NVT_NH
Then, in this NVT molecular dynamics
the temperature for nuclear motion can be controlled by
<MD.TempControl
3
100 2 1000.0 0.0
400 10 700.0 0.4
700 40 500.0 0.7
MD.TempControl>
The beginning of the description must be ' MD.TempControl',
and the last of the description must be 'MD.TempControl
MD.TempControl',
and the last of the description must be 'MD.TempControl '.
The first number '3' gives the number of the following lines
to control the temperature. In this case you can see that
there are three lines. Following the number '3',
in the consecutive lines the first column
means MD steps and the second column gives an interval
of MD steps that the velocity scaling is made.
For the example above, a velocity scaling is performed
at every two MD steps until 100 MD steps, at every 10 MD steps from 100
to 400 MD steps, and at every 40 MD steps from 400 to 700
MD steps. The third and fourth columns give a given temperature
'.
The first number '3' gives the number of the following lines
to control the temperature. In this case you can see that
there are three lines. Following the number '3',
in the consecutive lines the first column
means MD steps and the second column gives an interval
of MD steps that the velocity scaling is made.
For the example above, a velocity scaling is performed
at every two MD steps until 100 MD steps, at every 10 MD steps from 100
to 400 MD steps, and at every 40 MD steps from 400 to 700
MD steps. The third and fourth columns give a given temperature
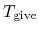 (K) and a scaling parameter
(K) and a scaling parameter 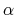 in the interval,
while the temperature in the interval is given by a linear
interpolation.
In this velocity scaling, the velocity is scaled by
where
in the interval,
while the temperature in the interval is given by a linear
interpolation.
In this velocity scaling, the velocity is scaled by
where 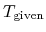 and
and 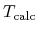 are a given and
calculated temperatures, respectively.
In 'NVT_VS' the temperature is calculated by using velocities of all the atoms.
On the other hand, the local temperature is estimated by the velocity of each atom
in 'NVT_VS2', and the velocity scaling is performed by the local temperature.
After the final MD step given in the specification
'MD.TempControl', the NVT ensemble is switched to a NVE ensemble.
Calculated quantities at every MD step are stored in an output
file 'System.Name.ene', where 'System.Name' means 'System.Name'.
Although you can find the details in 'iterout.c',
several quantities are summarized for your convenience as follows:
are a given and
calculated temperatures, respectively.
In 'NVT_VS' the temperature is calculated by using velocities of all the atoms.
On the other hand, the local temperature is estimated by the velocity of each atom
in 'NVT_VS2', and the velocity scaling is performed by the local temperature.
After the final MD step given in the specification
'MD.TempControl', the NVT ensemble is switched to a NVE ensemble.
Calculated quantities at every MD step are stored in an output
file 'System.Name.ene', where 'System.Name' means 'System.Name'.
Although you can find the details in 'iterout.c',
several quantities are summarized for your convenience as follows:
1: MD step
2: MD time
14: kinetic energy of nuclear motion, Ukc (Hartree)
15: DFT total energy, Utot (Hartree)
16: Utot + Ukc (Hartree)
17: Fermi energy (Hartree)
18: Given temperature for nuclear motion (K)
19: Calculated temperature for nuclear motion (K)
22: Nose-Hoover Hamiltonian (Hartree)
which means that the first and second columns correspond to
MD step and MD time, and so on.
As an example, we show a result for the velocity scaling MD
of a glycine molecule in Fig. 12 (a).
We see that the temperature in a molecule oscillates
around the given temperature.
Also for visualization of molecular dynamics,
an output file 'System.Name.md' can be easily animated using free software
OpenMX Viewer [152,151] and XCrySDen [105].
Figure 12:
(a) Given and calculated temperatures of a glycine molecule
as a function of MD steps
in a velocity scaling NVT molecular dynamics.
(b) Given and calculated temperatures of a glycine molecule
as a function of MD steps
in the Nose-Hoover NVT molecular dynamics.
The input files are 'Gly_VS.dat' and 'Gly_NH.dat'
in the directory 'work', respectively.
|
|
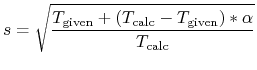
![\includegraphics[width=17.0cm]{Gly_MD.eps}](img154.png)