Next: Example Up: Computing Chern number and Previous: Computing Chern number and Contents Index
In OpenMX Ver. 3.9, a post-processing code 'calB' is supported to calculate the Chern number and Berry curvature of bands using overlap matrix elements between Kohn-Sham orbitals at neighboring k-points by the Fukui-Hatsugai-Suzuki method [81,85]. The functionality is compatible with only the non-collinear calculations. To acknowledge in any publications by using the functionality, the citation of the reference [84] would be appreciated.
The Chern number is a topological invariant being an integer number,
which characterizes the topology of bands for any materials.
In systems having a finite Chern number ![]() , the anomalous Hall conductivity defined by
, the anomalous Hall conductivity defined by
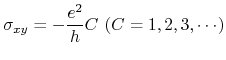 |
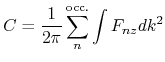 |
![\includegraphics[width=9.0cm]{Chern-Fig1.eps}](img457.png)
|
As shown in Fig. 73, the Berry curvature can be calculated in each 'plaquette'
(plaquette means meshed area in Brillouin zone) on a regular mesh
introduced in the first Brillouin zone by the following formula:
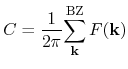 |