Next: Compilation of jx Up: Exchange coupling parameter Previous: Exchange coupling parameter Contents Index
The 'jx', a post-processing code for OpenMX, provides a way to calculate exchange coupling parameters ![]() between two localized spins based on Green's function representation of Liechtenstein formula [17].
In the standard distribution of OpenMX Ver. 3.9, the evaluation is supported for only
the collinear calculations of cluster and bulk systems.
To acknowledge in any publications by using the functionality, the citation of the references [18,19]
would be appreciated.
between two localized spins based on Green's function representation of Liechtenstein formula [17].
In the standard distribution of OpenMX Ver. 3.9, the evaluation is supported for only
the collinear calculations of cluster and bulk systems.
To acknowledge in any publications by using the functionality, the citation of the references [18,19]
would be appreciated.
The program provides three ways to calculate ![]() as explained below.
as explained below.
For cluster systems, the program computes exchange coupling constants ![]() between
atomic sites
between
atomic sites ![]() and
and ![]() from the following formula:
from the following formula:
For bulk systems, the program computes exchange coupling constants
![]() between individual sites
between individual sites ![]() and
and ![]() located at cells
located at cells ![]() and
and ![]() , respectively,
from the following formula:
, respectively,
from the following formula:
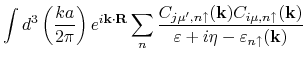 |
(6) | ||
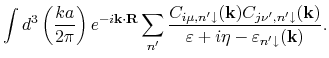 |
(7) |
Alternatively, it is also possible to compute the summation of exchange coupling ![]() over
over ![]() by the following formula:
by the following formula:
![\includegraphics[width=16cm]{jx_schematics.eps}](img251.png)
|
For users, it might be helpful to explain the difference between Eqs. (5)
and (8) by schematics shown in Fig. 37.
Figure 37 (a) shows a schematic of interaction between individual sites,
which corresponds to Eq. (5).
Figure 37 (b) shows a schematic of interaction between periodic images,
which corresponds to Eq. (8).
When executing, this option can be specified by Flag.PeriodicSum,
as explained in the latter subsection.