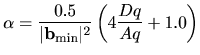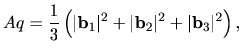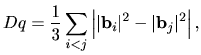



Next: On-the-fly control of SCF
Up: SCF convergence
Previous: General
Contents
Index
If the keyword 'scf.Kerker.factor' is not given in your input file,
OpenMX Ver. 3.7 automatically estimates a proper value of Kerker's factor 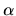 by the following
equation:
by the following
equation:
with
where
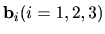 is a reciprocal vector, and
is a reciprocal vector, and
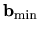 is the smallest vector
among {b}. The equation takes account of the dependency of
is the smallest vector
among {b}. The equation takes account of the dependency of 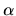 on the size and anisotropy
of the system. From a series of numerical calculations it is found that the estimated value works
well in most cases.
on the size and anisotropy
of the system. From a series of numerical calculations it is found that the estimated value works
well in most cases.
t-ozaki
2013-05-22
![]() by the following
equation:
by the following
equation: