Let us show effects of ESMs on the electronic structure of a system.
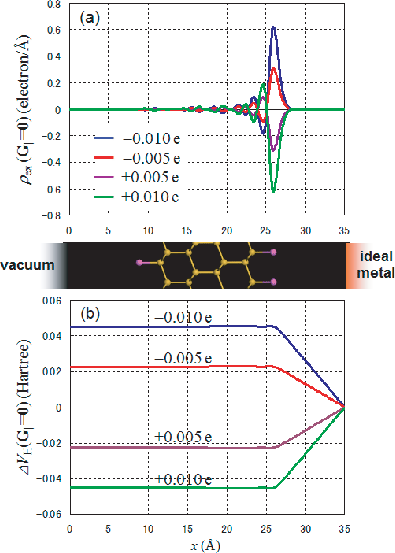
As a demonstration calculation, the distribution of excess charge ![]() in a
in a ![]() Al-terminated Si(111) slab under the boundary condition,
'vacuum + ideal metal' (ESM.switch = on3), is presented in Fig. 38(a)
(the input file of this test calculation 'Al-Si111_ESM.dat' is found
in the work directory).
It can be seen that segregation of the doped charge
in the slab happened due to the attractive interaction between the
doped and the corresponding mirror charges. Figure 38(b)
indicates the change of the Hartree potential
Al-terminated Si(111) slab under the boundary condition,
'vacuum + ideal metal' (ESM.switch = on3), is presented in Fig. 38(a)
(the input file of this test calculation 'Al-Si111_ESM.dat' is found
in the work directory).
It can be seen that segregation of the doped charge
in the slab happened due to the attractive interaction between the
doped and the corresponding mirror charges. Figure 38(b)
indicates the change of the Hartree potential
![]() corresponding to
each condition indicated in Fig. 38(a), where the potential inside the
Al-Si(111) slab and the electric field between the slab and the ideal-metal
medium change according to the amount of the doped charge.
corresponding to
each condition indicated in Fig. 38(a), where the potential inside the
Al-Si(111) slab and the electric field between the slab and the ideal-metal
medium change according to the amount of the doped charge.
 |