Divide-conquer method

The DC method is a robust scheme and can be applicable to a wide variety of materials with a reasonable degree of accuracy and efficiency, while this scheme is suitable especially for covalent systems. In this subsection, the O($N$) calculation using the DC method is illustrated. In an input file 'DIA8_DC.dat' which can be found in the directory 'work', please specify DC for the keyword 'scf.EigenvalueSolver'.

     scf.EigenvalueSolver   DC

Then, one can execute OpenMX by:

    % ./openmx DIA8_DC.dat
  

This input file is for an O($N$) calculation (1 MD step) of the diamond including 8 carbon atoms. The computational time is 248 seconds using a Xeon machine (3.0 GHz). Figure 15 shows the computational time and memory size to calculate a MD step of the carbon diamond as a function of number of atoms in the supercell. In fact, we see that the computational time and memory size are almost proportional to the number of atoms.

The accuracy and efficiency of the DC method are controlled by two simple parameters: 'orderN.HoppingRanges' and 'orderN.NumHoppings'.

• orderN.HoppingRanges

  The keyword 'orderN.HoppingRanges' defines the radius of a sphere which is centered on each atom. The logically truncated cluster for each atom is constructed for the atoms inside the sphere.

• orderN.NumHoppings

  The keyword 'orderN.NumHoppings' gives the number, $n$, of hopping which is required to construct the logically truncated cluster. The cluster of size, $n$, is defined by all neighbors that can be reached by $n$ hops, where the cutoff distance is given by the sum of the cutoff distances $r_1$ and $r_2$ of basis orbitals belonging to atoms 1 and 2.

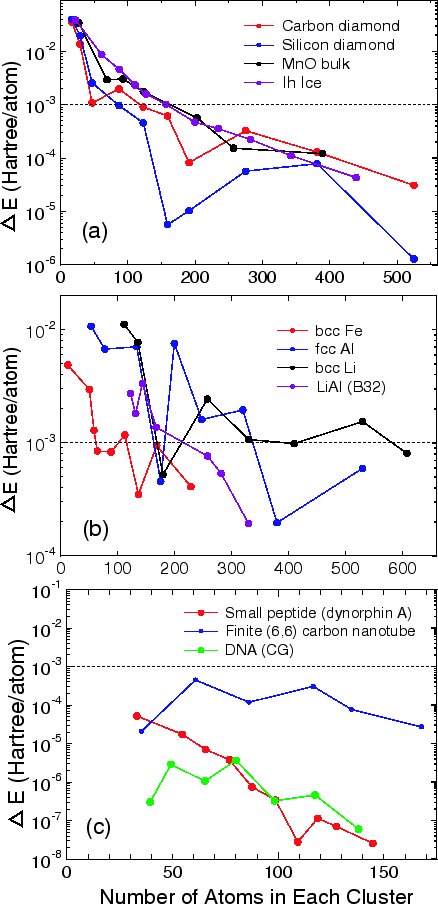
If the number of atoms in the systems is N, N small eigenvalue problems for the N logically truncated clusters are solved, and then the total density of states (DOS) is constructed as the sum of the projected DOS of each logically truncated cluster. Although the appropriate values for 'orderN.HoppingRanges' and 'orderN.NumHoppings' depend on systems, for molecular systems the following values are recommended as a trade-off between the computational accuracy and efficiency:

     orderN.HoppingRanges     6.0 - 7.0
     orderN.NumHoppings           2

Table 2 shows the comparison in the total energy between the exact diagonalization and the DC method for a C$_{60}$ molecule and small peptide molecules (valorphin [58]), and DNA consisting of cytosines and guanines. We find that errors in the total energy calculated by the DC method are about a few mHartree in the system size. Also, it can be estimated that the DC method is faster than the conventional diagonalization when the number of atoms is larger than 500 atoms, while the crossing point between the conventional diagonalization and the DC method with respect to computational time depends on systems and the number of processors in parallel calculations.

To see an overall tendency in the convergence properties of total energy with respect to the size of truncated cluster, the error in the total energy, compared to the exact diagonalization, is shown as a function of the number of atoms in each cluster for (a) bulks with a finite gap, (b) metals, and (c) molecular systems in Fig. 16. We see that the error decreases almost exponentially for the bulks with a finite gap and molecular systems, while the convergence speed is slower for metals.

Figure 15: Elapsed time of the diagonalization part per SCF step and computational memory size per MPI process as a function of carbon atoms in the diamond supercell, where 8 processes were used in the MPI parallel calculations. C5.0-s1p1 was used as basis orbitals. For the DC method, orderN.HoppingRanges=6.0 (Å) and orderN.NumHoppings=1 are used. A Xeon machine (3.0 GHz) was used to measure the elapsed time. The input files are DIA8_DC.dat, DIA64_DC.dat, DIA216_DC.dat, and DIA512_DC.dat in the directory 'work'.

Figure 16: Error in the total energy of (a) bulks with a finite gap, (b) metals, and (c) molecular systems calculated by the divide-conquer (DC) method as a function of the number of atoms in each cluster. The dotted horizontal line indicates 'milli-Hartree' accuracy.

Table 2: Total energy and computational time per MD step of a C$_{60}$ molecule and small peptide molecules (valorphin [58]) and DNA consisting of cytosines and guanines calculated by the conventional diagonalization and the O($N$) DC method, where a minimal basis set was used. In this Table, numbers in the parenthesis after DC means orderN.HoppingRanges and orderN.NumHoppings used in the DC calculation. The computational times were measured using an Opteron PC cluster (48 cpus $\times$ 2.4 GHz). The input files are C60_DC.dat, Valorphin_DC.dat, CG15c_DC.dat in the directory 'work'.

	Total energy (Hartree)	Computational time (s)
C$_{60}$
(60 atoms, 240 orbitals)
Conventional	-343.89680	36
DC (7.0, 2)	-343.89555	37
Valorphin
(125 atoms, 317 orbitals)
Conventional	-555.28953	81
DC (6.5, 2)	-555.29019	76
DNA
(650 atoms, 1880 orbitals)
Conventional	-4090.95463	576
DC (6.3, 2)	-4090.95092	415