 |
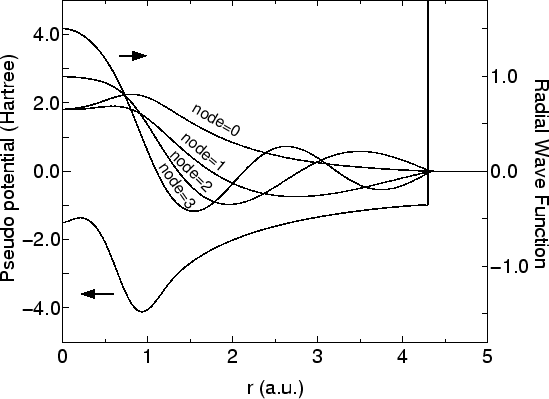
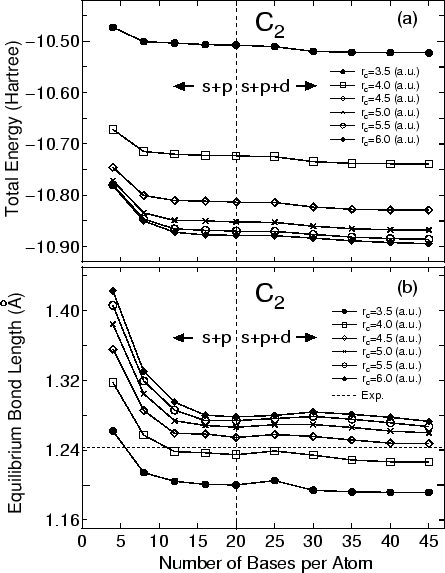
The primitive basis functions are generated by ADPACK, and they are the ground and exited states of a pseudo-atom with a confinement pseudopotential [26] shown in Fig. 1. The functions are numerical table function stored in a file of which file extension is 'pao'. You will see that the ground state is nodeless and the first exited state has one node, and the number of nodes increases in the further excited states. When you use the primitive PAO functions as basis set, the one-particle Kohn-Sham functions are expressed by the linear combination of the atomic type basis functions where each basis function is the product of the radial function and a real spherical harmonics function. The accuracy and efficiency of the calculations can be controlled by two parameters: a cutoff radius of basis orbitals and the number of basis orbitals. In general, one can get the convergent results by increasing the cutoff radius and the number of basis functions as shown in Fig. 2. However, note that the use of a large number of basis orbitals with large cutoff radii requires an extensive computational resource such as memory size and computational time. The general trend to choose the cutoff radius of basis orbitals and the number of basis orbitals in a compromise way is discussed in Ref. [26], where you may find that basis orbitals with a higher angular momentum are needed to achieve the sufficient convergence for elements, such as F and Cl, in the right side of the periodic table, and that a large cutoff radius of basis orbitals should be used for elements, such as Li and Na, in the left side of the periodic table. Since optimized basis functions are available on the web site (http://www.openmx-square.org/) as database Ver. 2011. We recommend for general users to use these optimized basis functions instead of the primitive PAO functions.
 |
 |