Krylov subspace method

The DC and GDC methods are robust and accurate for a wide variety of systems. However, to obtain an accurate result the size of truncated clusters tends to be large for metallic systems as shown in Fig. 16. A way of reducing the computational efforts is to map the original vector space defined by the truncated cluster into a Krylov subspace of which dimension is smaller than that of the original space [25]. The Krylov subspace method is available by

     scf.EigenvalueSolver       Krylov

Basically, the accuracy and efficiency are controlled by the following three keywords:

    orderN.HoppingRanges         6.0
    orderN.NumHoppings            2
    orderN.KrylovH.order         400

The keywords 'orderN.HoppingRanges' and 'orderN.NumHoppings' define the radius of a sphere centered on each atom and the number of hopping in the same sense as those in the DC and GDC methods. The dimension of Krylov subspace of Hamiltonian in each truncated cluster is given by the 'orderN.KrylovH.order'. Moreover, the Krylov subspace method can be precisely tuned by the following keywords:

Figure: (a) absolute error, with respect to the band calculations, in the total energy (Hartree/atom) calculated by the proposed and DC methods for metals and finite gap systems, (b) computational time (s/atom/MD). For a substantial comparison, the calculations were performed using a single Xeon processor. The set of numbers in the parenthesis of (a) means the average number of atoms in the core and buffer regions. The set of numbers in the parenthesis of (b) means the percentage of the dimension of the subspaces relative to the total number of basis functions in the truncated cluster, respectively.

• orderN.Exact.Inverse.S on$\vert$ off, default=on

  In case of 'orderN.Exact.Inverse.S=on', the inverse of overlap matrix for each truncated cluster is exactly evaluated. Otherwise, see the next keyword 'orderN.KrylovS.order'.

• orderN.KrylovS.order 1200, default=orderN.KrylovH.order$\times 4$

  In case of 'orderN.Exact.Inverse.S=off', the inverse is approximated by a Krylov subspace method for the inverse, where the dimension of the Krylov subspace of overlap matrix in each truncated cluster is given by the keyword 'orderN.KrylovS.order'.

• orderN.Recalc.Buffer on$\vert$ off, default=off

  In case of 'orderN.Recalc.Buffer=on', the buffer matrix is recalculated at every SCF step. Otherwise, the buffer matrix is calculated at the first SCF step, and fixed at subsequent SCF steps.

• orderN.Expand.Core on$\vert$ off, default=on

  In case of 'orderN.Expand.Core=on', the core region is defined by atoms within a sphere with radius of $1.2\times r_{\rm min}$, where $r_{\rm min}$ is the distance between the central atom and the nearest atom. In case of 'orderN.Expand.Core=off', the central atom is considered as the core region.

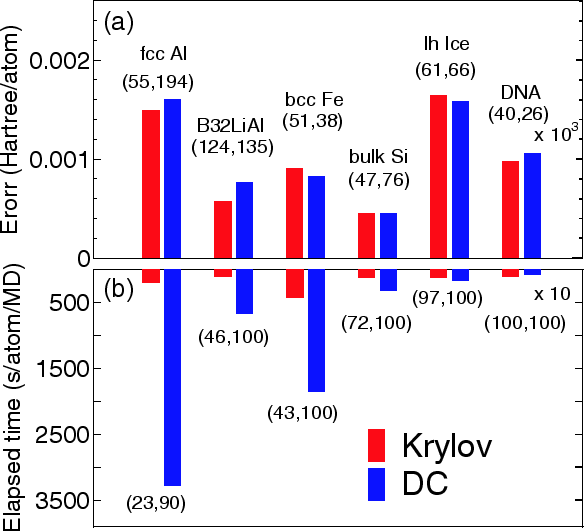
It is better to switch on 'orderN.Exact.Inverse.S' and 'orderN.Expand.Core' as the covalency increases, while the opposite could becomes better in simple metallic systems. In Fig. 17 the absolute error in the total energy calculated by the Krylov and DC methods are shown for a wide variety of materials. It is found that in comparison with the DC method, the Krylov subspace method is more efficient especially for metallic systems, and that the efficiency become comparable as the covalency and ionicity in the electronic structure increase.